Diagrama de Diagnostico para Cromosferas Estelares

Francisco Tapia Vázquez, Victor De la Luz, Luis Zapata, Jacob White

Última actualización el Oct 5, 2023 7 min de lectura Blog

“Imagen” de Altair a 33 GHz obtenida con el Very Large Array. (White et al., 2021)

Introducción

Los espectros en radio de las estrellas de la secuencia principal permanecen en gran medida sin restricciones debido a la falta de datos de observación para ajustar modelos de atmósferas estelares. Los mecanismos de emisión dominantes a longitudes de onda largas, cómo varían con el tipo espectral y cuánto contribuyen al brillo esperado a una longitud de onda de radio determinada aún son relativamente desconocidos para la mayoría de las clases espectrales estelares. Las características particulares de la emisión en longitudes de onda milimétricas, submilimétricas e infrarrojas en la cromosfera solar nos permiten estimar su temperatura y densidad utilizando metodologías indirectas como modelos semiempíricos (Vernazza et al. 1981; Fontenla et al. 1993; Avrett & Loeser 2008). Estos modelos son una herramienta importante para un amplio conjunto de estudios, por ejemplo, cromosferas solares y estelares (Loukitcheva et al. 2004; Linsky 2017), temperatura mínima (Liseau et al. 2013; De la Luz et al. 2014), erupciones solares (Machado et al. 1980; Trottet et al. 2015) y características de los componentes de Sun (Fontenla et al. 2006).

Los modelos semiempíricos predicen valores cercanos a las temperaturas fotosféricas que disminuyen hasta un mínimo, luego aumentan dramáticamente hasta las coronas (Vernazza et al. 1981; Avrett & Loeser 2008. Esta capa se conoce como la cromosfera solar. La cromosfera permanece observable por diferentes rangos espectrales que incluyen el ultravioleta en la emisión continua y lineal, en el visible (principalmente Hα) y en las longitudes de onda milimétrica, submilimétrica e infrarroja. Este último rango de longitud de onda se vuelve más importante a medida que se realizan mejoras en la sensibilidad y la resolución espacial en los radiotelescopios modernos (Nakajima et al. 1995; Kudaka et al. 2015; Wedemeyer et al. 2016).

Modelo semiempírico de laa atmósfera del Sol. Copyright: walsa.team

En este trabajo presentamos una nueva relación entre la temperatura mínima y la temperatura efectiva de la estrella. Utilizamos los modelos obtenidos con KINICH PAKAL (Tapia-vázquez & De la Luz, 2020) para construir una grilla de modelos semiempíricos. Además, construimos una malla de temperatura de brillo observada. La ubicación precisa de la temperatura mínima depende de la estructura detallada de la atmósfera y, sin una teoría convincente a mano, solo puede determinarse a partir de la medición directa. Es en esta región donde se deposita la energía no radiativa, y su física es de gran interés general (Liseau et al. 2013).

Métodos

Nuestro trabajo se basa en modelos previos de estrellas de secuencia principal obtenidos a partir de observaciones de longitudes de onda FIR a mm (White et al. 2021; White et al. 2020; Tapia-Vázquez & De la luz, 2020).

Observaciones

Las observaciones a frecuencias superiores a 1000 GHz se obtuvieron del archivo de datos de Herschel. Las observaciones entre 1000 GHz y 90 GHz provinieron de ALMA y NOEMA. Para frecuencias bajas como 33 GHz y 17 GHz, las observaciones se realizaron con VLA y ATCA.

En la literatura podemos (Villadsen et al. 2014, Liseau et al. 2016, White et al. 2018, Rodríguez et al. 2019, White et al. 2020, White et al. 2021)

Imáagenes obtenidas con el radio-interferómetro ALMA. (White et al. 2020)

Espectro obtenido a longitudes de onda milimétricas, sub-milimétricas e infrarrojas. (White et al. 2021)

KINICH PAKAL

En el infrarrojo lejano/longitudes de onda milimétricas, la emisión estelar en las estrellas de la secuencia principal está dominada por una radiación libre-libre ópticamente gruesa (Dulk 1985; Güdel 2002). El flujo es proporcional a la temperatura del plasma ($T_{R}$) a una determinada longitud de onda y se puede utilizar para sondear la estructura de la temperatura en función de la altura sobre la fotosfera. Por lo tanto, el espectro estelar se puede utilizar para construir un modelo de la estructura térmica de la cromosfera. Estos modelos se generaron utilizando el código KINICH-PAKAL (Tapia-Vázquez & De la Luz 2020). Este código modifica iterativamente los perfiles radiales de temperatura y densidad de hidrógeno, el balance de ionización y la opacidad de un modelo base usando el algoritmo de Levenberg-Marquardt para ajustar el espectro sintético a los datos de ALMA presentados aquí y los datos de Herschel/PACS para γ Lep ( Montesinos et al. 2016). En la atmósfera, la cromosfera tiene una temperatura más alta que la fotosfera, lo que provoca una fuerte desviación del equilibrio radiativo. Por lo tanto, no asumimos que la ionización-excitación y la transferencia radiativa están en equilibrio térmico local. Para nuestros modelos, se adoptó como punto de partida un modelo solar semiempírico (modelo C7 de Avrett & Loeser 2008) en equilibrio hidrostático. Esto se puede tomar como un promedio de los modelos solares más utilizados. (Vernazza et al. 1981; Fontenla et al. 1993; Loukitcheva et al. 2004). Para estrellas con una temperatura efectiva superior a la del Sol, este modelo sirve como condición inicial.

Resultados

Malla de observación

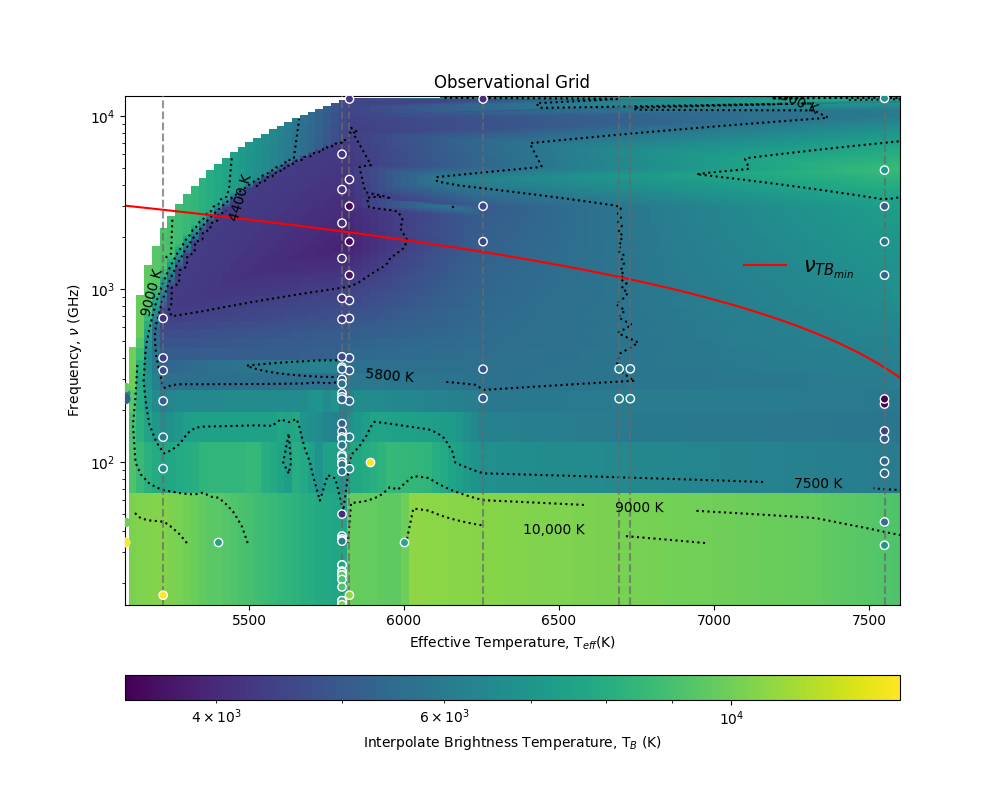
En la figura 1 mostramos la malla de observación obtenida a partir de la interpolación de 11 estrellas encontradas en la literatura. Mientras que la temperatura efectiva va aumentando, la frecuencia en la que se encuentra la temperatura mínima se va acercando a las bajas frecuencias. Este comportamiento se puede caracterizar mediante la ecuación

$$ \begin{equation} \label{eq:obs_grid} \nu_{T_{B_{min}}}(T_{eff}) = a log(b T_{eff}) + c \end{equation} $$

Dónde

$\nu$ es la frecuencia observada
$T_{B_{min}}$ es la temperatura mínima de brillo
$T_{eff}$ es la temperatura efectiva de inicio
a=-6,81$x10^{3}$
b=1.41$x10^{-3}$
c=1,65$x10^{4}$

Malla de modelo semiempírico

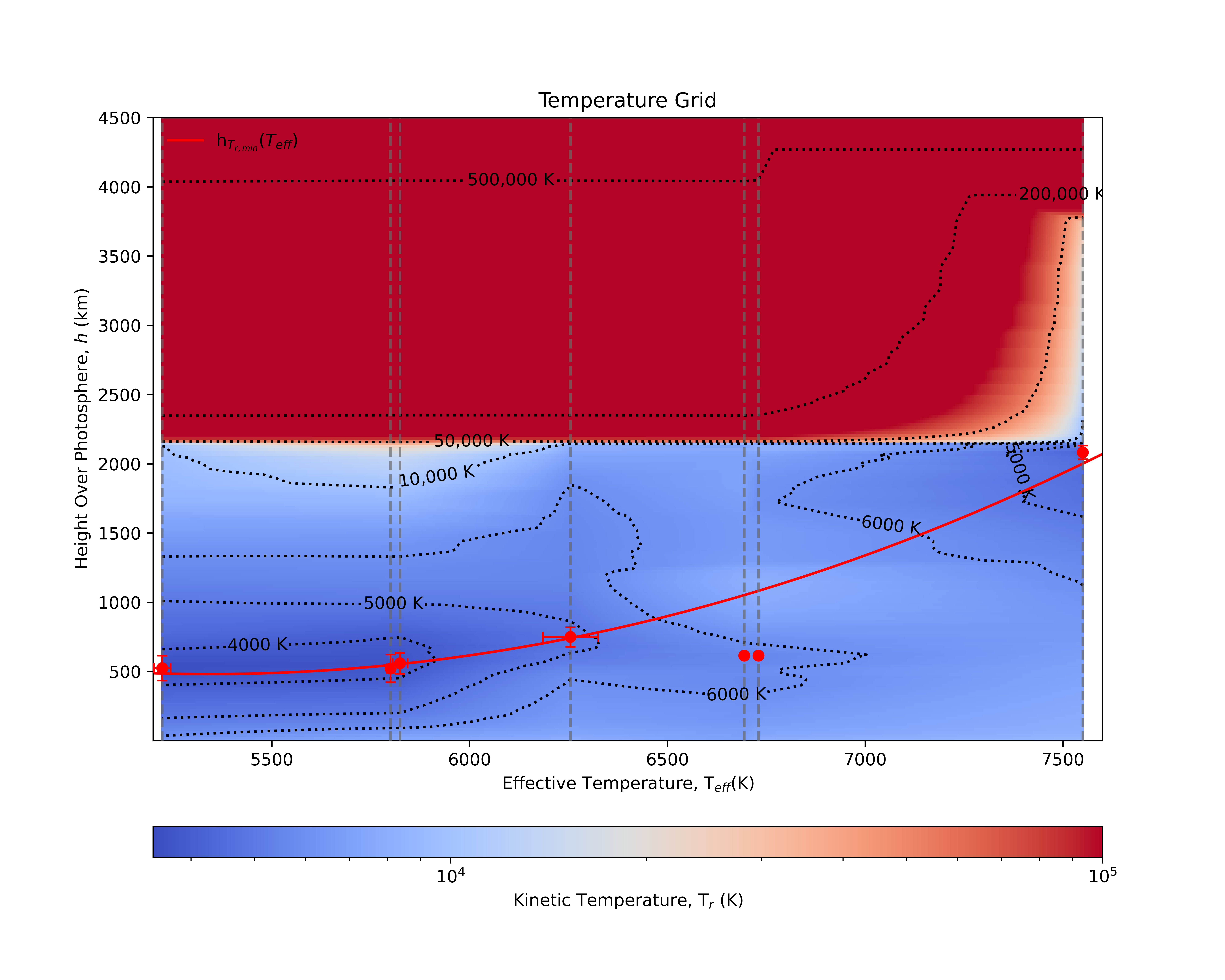
La Figura 2 muestra el modelo de grilla sempiempírico. Esta malla está compuesta por los modelos semipíricos publicados para 7 estrellas, incluido el sol. Para las estrellas desaparecidas no fue posible obtener un modelo confiable, principalmente debido a la falta de observaciones. Como ejemplo tenemos $\tau$ Cet que fue observado por Villadessen et al., (2014). En esa ocasión se detectó a 33 GHz y no a 15 GHz, por lo que no es factible construir un modelo, ya que solo estaríamos modelando una región muy pequeña de la atmósfera.

$$ \begin{equation} \label{eq:minimo} h_{T_{r,min}}(T_{eff}) = aT_{eff}+ bT_{eff}^2 +c \end{equation} $$

Dónde

h es la altura a la que se encuentra la temperatura mínima radial
$T_{r, min}$ es la temperatura radial mínima
$T_{eff}$ es la temperatura efectiva de inicio
a=-3.33
b=3,11x10$^{-4}$
c=9.37x10$^3$

Figure 2. Malla de modelos semiempíricos. La línea roja indica la relación entre el mínimo de temperatura y la temperatura efectiva de la estrella.

Conclusión

Encontramos una relación entre la temperatura radial mínima y la temperatura efectiva de la estrella.
La frecuencia con la que se encuentra la temperatura mínima observada varía con la temperatura efectiva de la estrella.