Introduction

The radio spectra of main-sequence stars remain largely unconstrained due to the lack of observational data to inform stellar atmosphere models. As such, the dominant emission mechanisms at long wavelengths, how they vary with spectral type, and how much they contribute to the expected brightness at a given radio wavelength are still relatively unknown for most spectral types. The particular characteristics of the emission at millimeter, submillimeter, and infrared wavelengths in the solar chromosphere allow us to estimate their temperature and density using indirect methodologies like semiempirical models (Vernazza et al. 1981; Fontenla et al. 1993; Avrett & Loeser 2008). These models are an important tool for a wide set of studies, e.g., solar and stellar chromospheres (Loukitcheva et al. 2004;Linsky 2017), temperature minimum (Liseau et al. 2013; De la Luz et al. 2014), solar flares (Machado et al. 1980; Trottet et al. 2015), and Sun component features (Fontenla et al. 2006).

Semiempirical models predict values close to photospheric temperatures that decrease until a minimum, then increase dramatically until the coronae (Vernazza et al. 1981; Avrett & Loeser 2008. This layer is known as the solar chromosphere. The chromosphere remains observable by different spectral ranges that include ultraviolet in the continuum and line emission, in the visible (mainly Hα), and in the millimeter, submillimeter, and infrared wavelengths. This last wavelength range becomes more important as improvements in the sensitivity and space resolution in modern radio telescopes are made (Nakajima et al. 1995; Kudaka et al. 2015; Wedemeyer et al. 2016).

In this work, we present a new relation between temperature minimum and effective temperaature of the star. We use the models obtained with KINICH PAKAL (Tapia-vázquez & De la Luz, 2020) to construct a grid of semiempirical models. Addicionally, we construct a grid of observed brightness temperature. The precise location of the temperature minimum depends on the detailed structure of the atmosphere and can, with no convincing theory at hand, only be determined from direct measurement. It is in this region where non-radiative energy is deposited, and its physics is of strong general interest (Liseau et al. 2013).

Methods

Our work is based in previous models of main sequence stars obtained from FIR to mm wavelenghts observations (White et al. 2021; White et al. 2020; Tapia-Vázquez & De la luz, 2020).

Observations

Observations at frequencies greater than 1000 GHz were obtained from Herschel data archival. Beetween 1000 GHz and 90 GHz observations came from ALMA and NOEMA. For low frequencies like 33 GHz and 17 GHz, observations were performand with VLA and ATCA.

In literature we can (Villadsen et al. 2014, Liseau et al. 2016, White et al. 2018, Rodríguez et al. 2019, White et al. 2020, White et al. 2021)

KINICH PAKAL

At far-infrared/millimeter wavelengths, stellar emission in main sequence stars is dominated by optically thick free–free radiation (Dulk 1985; Güdel 2002). The flux is proportional to the plasma temperature ($T_{R}$) at a given wavelength and can be used to probe the temperature structure as a function of height above the photosphere. The stellar spectrum can therefore be used to build a model of the thermal structure of the chromosphere. These models were generated using the KINICH-PAKAL code (Tapia-Vázquez & De la Luz 2020). This code iteratively modifies the radial temperature and hydrogen density profiles, the ionization balance, and the opacity of a base model using the Levenberg–Marquardt algorithm to adjust the synthetic spectrum to the ALMA data presented here and the Herschel/PACS data for γ Lep (Montesinos et al. 2016). In the atmosphere, the chromosphere has a higher temperature than the photosphere leading to a strong deviation from radiative equilibrium. Therefore, we do not assume that ionization-excitation and radiative transfer are in local thermal equilibrium. For our models, a semiempirical solar model (model C7 from Avrett & Loeser 2008) in hydrostatic equilibrium was adopted as the starting point. This can be taken as an average of the most commonly used solar models (Vernazza et al. 1981; Fontenla et al. 1993; Loukitcheva et al. 2004). For stars with a higher effective temperature than the Sun, this model serves as an initial condition.

Results

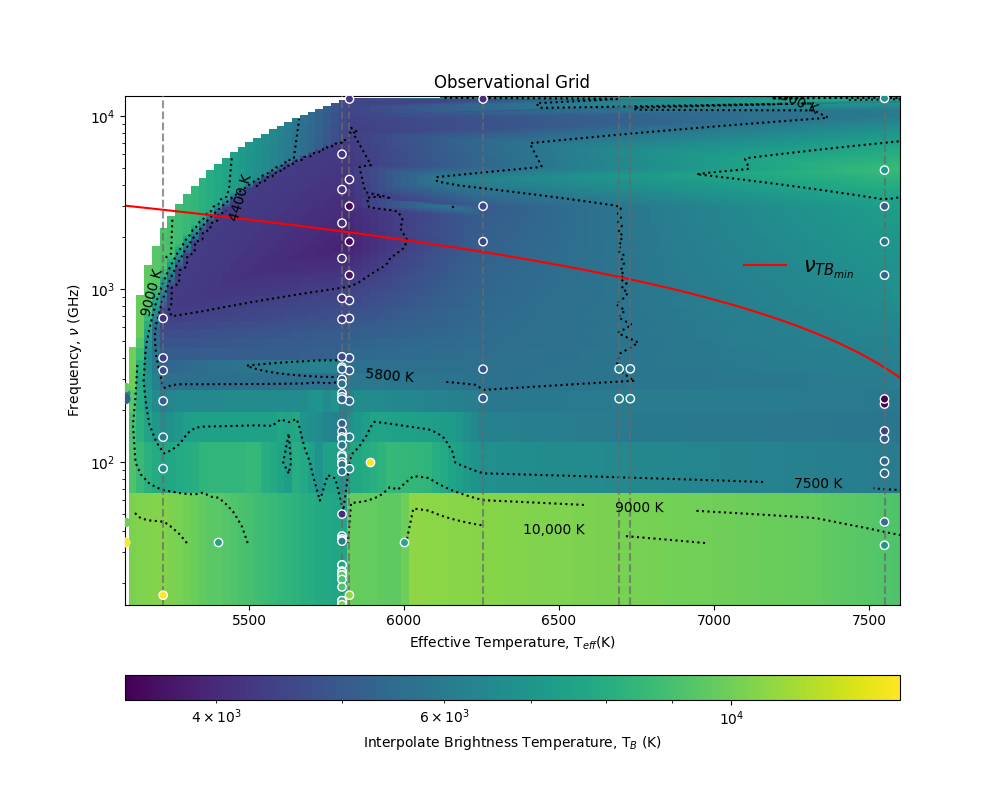
Observational grid

In figure 1, we show the observation grid obtained from the interpolation of 11 stars found in the literature. While the effective temperature is increasing, the frequency at which the minimum temperature is located is approaching the low frequencies. This behavior can be characterized using the equation

$$ \begin{equation} \label{eq:obs_grid} \nu_{T_{B_{min}}}(T_{eff}) = a log(b T_{eff}) + c \end{equation} $$

Where

• $\nu$ is the observed frequency
• $T_{B_{min}}$ is minimum brightness temperature
• $T_{eff}$ is the efective temperature of the start
• a=-6.81$x10^{3}$
• b=1.41$x10^{-3}$
• c=1.65$x10^{4}$

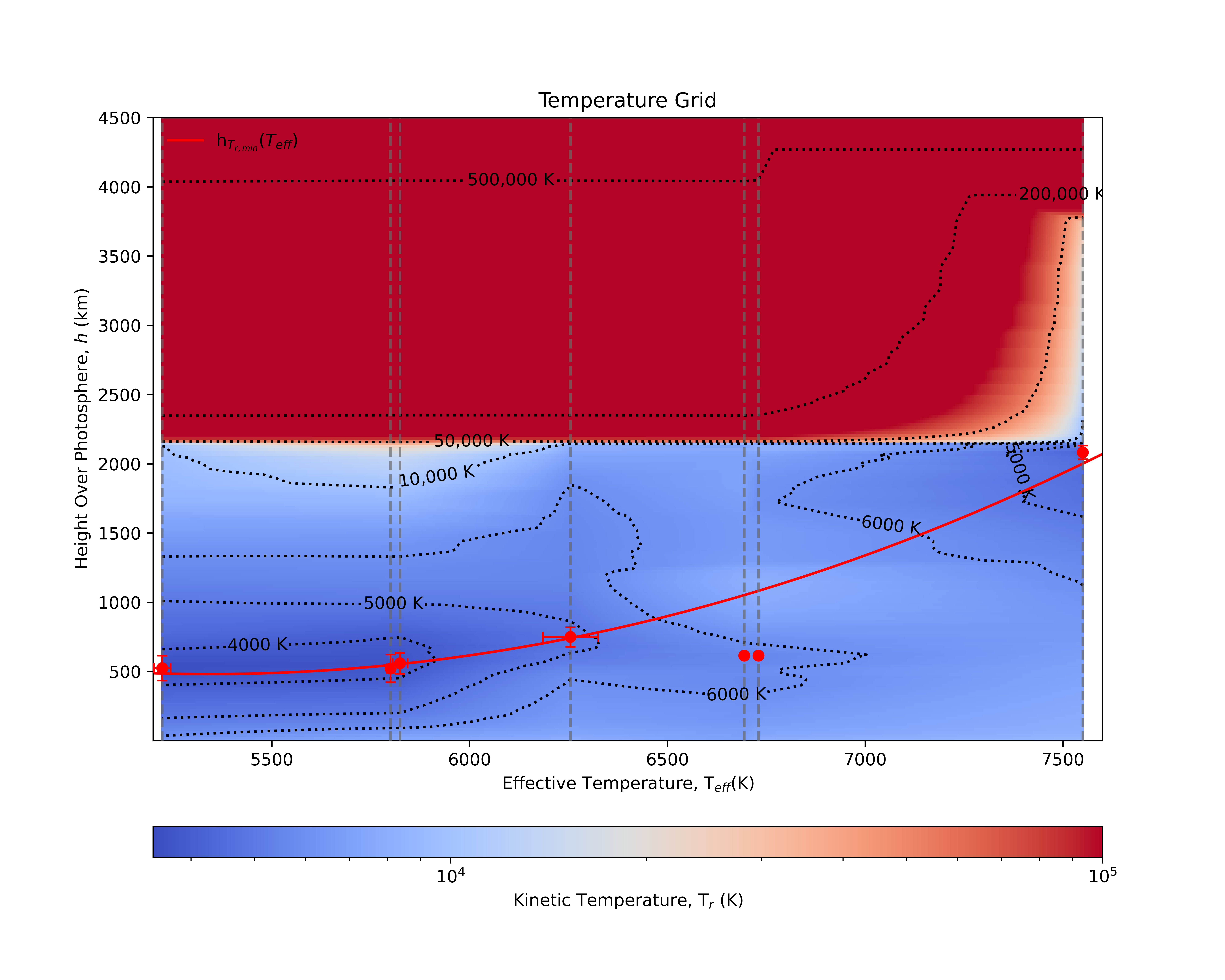
Semiempirical model grid

Figure 2 shows the sempiempirical grid model. This grid is composed of the published semipyrical models for 7 stars, including the sun. For the missing stars it was not possible to obtain a reliable model, mainly due to the lack of observations. As an example, we have $\tau$ Cet which was observed by Villadessen et al., (2014). On that occasion, it was detected at 33 GHz and not at 15 GHz, so building a model is not feasible, since we would only be modeling a very small region of the atmosphere.

$$ \begin{equation} \label{eq:minimo} h_{T_{r,min}}(T_{eff}) = aT_{eff}+ bT_{eff}^2 +c \end{equation} $$

Where

• h is the height at which the minimum radial temperature iss located
• $T_{r, min}$ is minimum radial temperature
• $T_{eff}$ is the efective temperature of the start
• a=-3.33
• b=3.11x10$^{-4}$
• c=9.37x10$^3$

Conclusion

• We found a relationship between the radial temperature minimum and the effective temperature of the star.
• The frequency at which the observed temperature minimum is found varies with the effective temperature of the star.

Acknowledgement

This work was supported by the Ciencia Básica (254497, bkhbvjkhfb) CONACyT Fellowship. The author thank to PAEP-UNAM fellowship.